Metallic materials are made into products through various working processes, such as casting, hot working, cold working, heat treatment, and plastic deformation. During these processes, material microstructures change significantly depending on the process conditions, and various material properties, such as mechanical properties, change depending on the changes in the material microstructure. Therefore, to improve the properties of materials, it is essential to appropriately control the microstructures.
In this laboratory, we develop computer-aided prediction techniques for material microstructures formed in a series of working processes, using various numerical models and numerical schemes. We are also clarifying the phenomena that occur during the formation process of material microstructures using numerical methods. In particular, we use the phase-field method as the main numerical model, which is the most powerful numerical model for expressing material microstructure evolution on a meso-scale. Furthermore, we conduct studies in which the phase-field method is applied for the prediction of material microstructures as well as to study various phenomena, such as crack propagation, topology optimization, and multi-phase flow.
Phase-field Method and its Large-scale Simulation

We perform material microstructure prediction simulations using the phase-field method and large-scale simulations using GPUs and supercomputers. In large-scale phase-field simulations, we have performed the world’s largest simulations of dendrite solidification and grain growth, and continue to produce results that can only be achieved by large-scale simulations.
Y. Shibuta, M. Ohno, T. Takaki, Advent of Cross-Scale Modeling: High-Performance Computing of Solidification and Grain Growth, Advanced Theory and Simulations 1 (2018) 1800065.
https://doi.org/10.1002/adts.201800065
Y. Shibuta, M. Ohno, T. Takaki, Solidification in a Supercomputer: From Crystal Nuclei to Dendrite Assemblages, JOM 67 (2015) 1793-1804.
https://link.springer.com/article/10.1007%2Fs11837-015-1452-2
T. Takaki, Phase-field modeling and simulations of dendrite growth, ISIJ International 54 (2014) 437-444.
https://doi.org/10.2355/isijinternational.54.437
T. Takaki, T. Shimokawabe, M. Ohno, A. Yamanaka, T. Aoki, Unexpected selection of growing dendrites by very-large-scale phase-field simulation, Journal of Crystal Growth 382 (2013) 21-25.
https://doi.org/10.1016/j.jcrysgro.2013.07.028
Competitive Growth of Columnar Dendrites
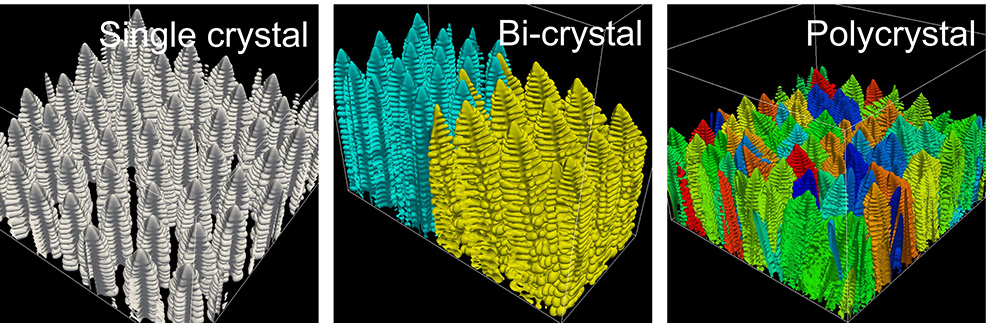
We have been conducting competitive growth simulations of columnar dendrites, where the dendrite spacing and alignment in single crystals, the mechanism of unusual selection in bi-crystals, and the formation mechanism of columnar structures in polycrystals have been investigated. This research has been made possible only through large-scale three-dimensional simulations using a supercomputer.
T. Takaki, S. Sakane, M. Ohno, Y. Shibuta, T. Aoki, C.-A. Gandin, Competitive grain growth during directional solidification of a polycrystalline binary alloy: Three-dimensional large-scale phase-field study, Materialia 1 (2018) 104-113.
https://doi.org/10.1016/j.mtla.2018.05.002
T. Takaki, S. Sakane, M. Ohno, Y. Shibuta, T. Shimokawabe, T. Aoki, Primary arm array during directional solidification of a single-crystal binary alloy: Large-scale phase-field study, Acta Materialia 118 (2016) 230-243.
http://dx.doi.org/10.1016/j.actamat.2016.07.049
T. Takaki, S. Sakane, M. Ohno, Y. Shibuta, T. Shimokawabe, T. Aoki, Large-scale Phase-field Studies of Three-dimensional Dendrite Competitive Growth at the Converging Grain Boundary during Directional Solidification of a Bicrystal Binary Alloy, ISIJ International 56(8) (2016) 1427-1435.
https://doi.org/10.2355/isijinternational.ISIJINT-2016-156
T. Takaki, M. Ohno, Y. Shibuta, S. Sakane, T. Shimokawabe, T. Aoki, Two-dimensional phase-field study of competitive grain growth during directional solidification of polycrystalline binary alloy, Journal of Crystal Growth 442 (2016) 14-24.
http://dx.doi.org/10.1016/j.jcrysgro.2016.01.036
T. Takaki, M. Ohno, T. Shimokawabe, T. Aoki, Two-dimensional phase-field simulations of dendrite competitive growth during the directional solidification of a binary alloy bicrystal, Acta Materialia 81 (2014) 272-283.
https://doi.org/10.1016/j.actamat.2014.08.035
Dendrite Growth with Liquid Flow

By coupling the phase-field and lattice Boltzmann method, we enabled simulations of dendrite growth with liquid flow. It is very important to consider liquid flow in solidification simulations of alloys because the solidification morphology varies significantly depending on natural and forced convection. However, owing to the high computational cost of liquid flow simulation, it is necessary to develop a more efficient numerical scheme to enable simulations on a realistic scale.
S. Sakane, T. Takaki, Phase-field lattice Boltzmann method with two-relaxation-time model for dendrite growth of a binary alloy with melt convection, Computational Materials Science 186 (2021) 110070.
https://doi.org/10.1016/j.commatsci.2020.110070
T. Takaki, S. Sakane, M. Ohno, Y. Shibuta, T. Aoki, Large-scale phase-field lattice Boltzmann study on the effects of natural convection on dendrite morphology formed during directional solidification of a binary alloy, Computational Materials Science 171 (2020) 109209.
https://doi.org/10.1016/j.commatsci.2019.109209
T. Takaki, S. Sakane, M. Ohno, Y. Shibuta, Competitive growth during directional solidification of a binary alloy with natural convection: two-dimensional phase-field study, Modelling and Simulation in Materials Science and Engineering 27 (2019) 054001.
https://doi.org/10.1088/1361-651X/ab1a17
S. Sakane, T. Takaki, M. Ohno, Y. Shibuta, T. Shimokawabe, T. Aoki, Three-dimensional morphologies of inclined equiaxed dendrites growing under forced convection by phase-field-lattice Boltzmann method, Journal of Crystal Growth 483 (2018) 147-155.
https://doi.org/10.1016/j.jcrysgro.2017.11.029
T. Takaki, R. Rojas, S. Sakane, M. Ohno, Y. Shibuta, T. Shimokawabe, T. Aoki, Phase-field-lattice Boltzmann studies for dendritic growth with natural convection, Journal of Crystal Growth 474 (2017) 146-153.
http://dx.doi.org/10.1016/j.jcrysgro.2016.11.099
S. Sakane, T. Takaki, R. Rojas, M. Ohno, Y. Shibuta, T. Shimokawabe, T. Aoki, Multi-GPUs parallel computation of dendrite growth in forced convection using the phase-field-lattice Boltzmann model, Journal of Crystal Growth 474 (2017) 154-159.
http://dx.doi.org/10.1016/j.jcrysgro.2016.11.103
R. Rojas, T. Takaki, M. Ohno, A phase-field-lattice Boltzmann method for modeling motion and growth of a dendrite for binary alloy solidification in the presence of melt convection, Journal of Computational Physics 298 (2015) 29-40.
http://dx.doi.org/10.1016/j.jcp.2015.05.045
Growth of Equiaxed Dendrites with Motion

The solidification structure can be roughly classified into columnar and equiaxed structures. Because equiaxed grains are isolated in the liquid phase, they move in the liquid phase owing to the solid-liquid density difference under gravity. Because this motion causes serious solidification defects such as segregation and cracking, it is necessary to represent the motion of the solid for reproducing the formation process of the equiaxed structure. In this study, the phase-field method was used for the first time to stably represent equiaxed dendrite growth with motion, and the method has been extended to polycrystalline solidification problems.
S. Sakane, T. Takaki, M. Ohno, Y. Shibuta, T. Aoki, Two-dimensional large-scale phase-field lattice Boltzmann simulation of polycrystalline equiaxed solidification with motion of a massive number of dendrites, Computational Materials Science 178 (2020) 109639.
https://doi.org/10.1016/j.commatsci.2020.109639
S. Sakane, T. Takaki, M. Ohno, Y. Shibuta, Simulation method based on phase-field lattice Boltzmann model for long-distance sedimentation of single equiaxed dendrite, Computational Materials Science 164 (2019) 39-45.
https://doi.org/10.1016/j.commatsci.2019.03.047
T. Takaki, R. Sato, R. Rojas, M. Ohno, Y. Shibuta, Phase-field lattice Boltzmann simulations of multiple dendrite growth with motion, collision, and coalescence and subsequent grain growth, Computational Materials Science 147 (2018) 124–131.
https://doi.org/10.1016/j.commatsci.2018.02.004
N. Yamanaka, S. Sakane, T. Takaki, Multi-phase-field lattice Boltzmann model for polycrystalline equiaxed solidification with motion, Computational Materials Science 197 (2021) 110658.
https://doi.org/10.1016/j.commatsci.2021.110658
Semi-solid Deformation
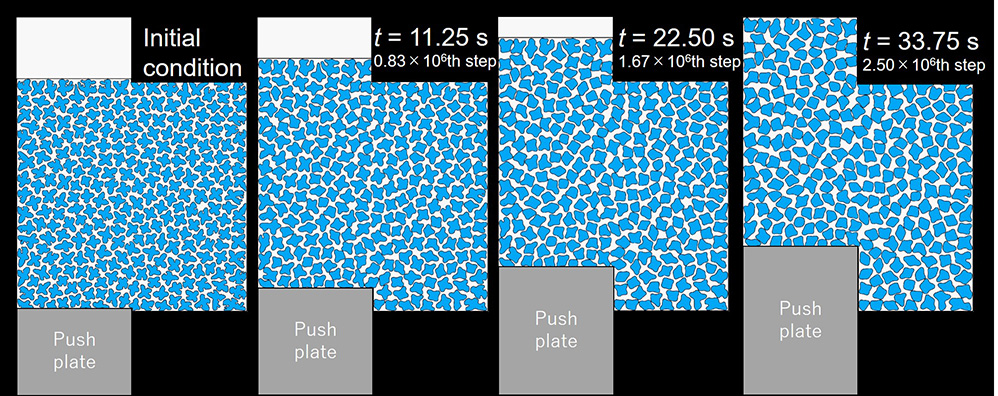
During solidification, alloys are subjected to external forces, such as solidification shrinkage, centrifugal force (centrifugal casting), press-in (die casting), gravity, and rolling (continuous casting). When equiaxed grains in a solid-liquid coexistence state are subjected to external forces, they behave differently from pure liquid and solid because of the interaction between solids depending on the solid fraction and grain shape. Among them, dilatancy is well known, which increases the apparent volume and causes segregation bands and cracks. Because the semi-solid deformation behaves in a peculiar way, our study is focused on modeling this phenomenon and clarifying it numerically.
N. Yamanaka, S. Sakane, T. Takaki, Multi-phase-field lattice Boltzmann model for polycrystalline equiaxed solidification with motion, Computational Materials Science 197 (2021) 110658.
https://doi.org/10.1016/j.commatsci.2021.110658
N. Yamanaka, S. Sakane, T. Takaki, Application of multi-phase-field lattice Boltzmann method to semi-solid deformation, IOP Conference Series: Materials Science and Engineering 861 (2020) 012067.
https://doi.org/10.1088/1757-899X/861/1/012067
Permeability for Flow of Interdendritic Liquid
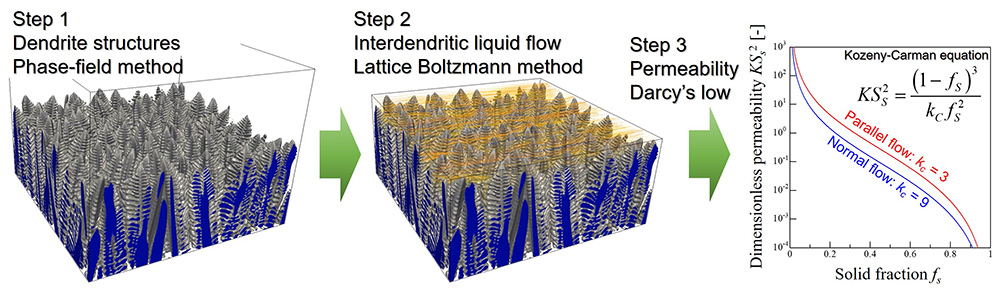
During the casting process of an alloy, the liquid flows with solidification. Solidification proceeds by dendrite growth, and thus the liquid flows between the dendrite network. Permeability is a measure of the flowability of a liquid through a dendrite network and is an important parameter in macroscale casting simulations. In this study, the permeability for the flow of an interdendritic liquid is estimated numerically. The computational procedure of permeability is as follows: the dendrite microstructure is obtained by the phase-field simulation (Step 1); the interdendritic liquid flow is computed using the lattice Boltzmann method (Step 2); and the permeability is computed based on Darcy’s law using the results of Step 2 (Step 3).
Y. Mitsuyama, T. Takaki, S. Sakane, Y. Shibuta, M. Ohno, Permeability tensor for columnar dendritic structures: Phase-field and lattice Boltzmann study, Acta Materialia 188 (2020) 282-287.
https://doi.org/10.1016/j.actamat.2020.02.016
T. Takaki, S. Sakane, M. Ohno, Y. Shibuta, T. Aoki, Permeability prediction for flow normal to columnar solidification structures by large–scale simulations of phase–field and lattice Boltzmann methods, Acta Materialia 164 (2019) 237-249.
https://doi.org/10.1016/j.actamat.2018.10.039
Development of AMR Phase-field Method

The phase-field method has the disadvantage of high computational cost because it requires fine meshes to express a smooth profile of the phase-field variable in the thin interface region. To reduce the computational cost and accelerate the simulation, we develop an adaptive mesh refinement (AMR) method for phase-field simulations, in which fine meshes are placed only near the interface and coarse meshes are used in other regions. In addition, we have applied the AMR phase-field method to multi-GPU parallel computation to achieve large-scale and high-speed computations.
Multi-phase-field Simulation of Grain Growth
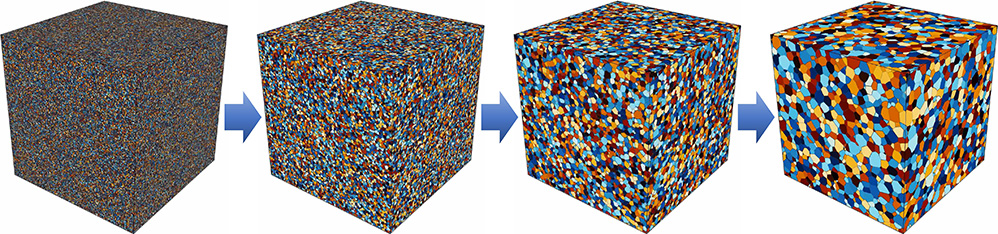
Solid metallic materials generally have polycrystalline structures. When they are heat-treated at high temperatures, grain growth occurs, in which the crystal grains become coarse. Heat treatment of plastically deformed metallic materials causes static recrystallization, whereas the hot working of metallic materials causes dynamic recrystallization. Grain growth also occurs during the recrystallization process. Thus, grain growth is an important phenomenon that determines the material microstructure of the final product. In this study, we simulate the grain growth and recrystallization of polycrystalline materials using the multi-phase-field method, which uses multiple phase-field variables.
E. Miyoshi, T. Takaki, S. Sakane, M. Ohno, Y. Shibuta, T. Aoki, Large-scale phase-field study of anisotropic grain growth: Effects of misorientation-dependent grain boundary energy and mobility, Computational Materials Science 186 (2021) 109992.
https://doi.org/10.1016/j.commatsci.2020.109992
E. Miyoshi, T. Takaki, M. Ohno, Y. Shibuta, Accuracy Evaluation of Phase-field Models for Grain Growth Simulation with Anisotropic Grain Boundary Properties, ISIJ International 60(1) (2020) 160-167.
https://doi.org/10.2355/isijinternational.ISIJINT-2019-305
E. Miyoshi, T. Takaki, M. Ohno, Y. Shibuta, S. Sakane, T. Shimokawabe, T. Aoki, Correlation between three-dimensional and cross-sectional characteristics of ideal grain growth: large-scale phase-field simulation study, Journal of Materials Science 53 (2018) 15165-15180.
https://doi.org/10.1007/s10853-018-2680-y
E. Miyoshi, T. Takaki, M. Ohno, Y. Shibuta, S. Sakane, T. Shimokawabe, T. Aoki, Ultra-large-scale phase-field simulation study of ideal grain growth, npj Computational Materials 3 (2017) 25.
https://doi.org/10.1038/s41524-017-0029-8
Data Assimilation Integrating MD and Phase-field Methods

As the performance of computers has improved, it is becoming possible to simultaneously perform two numerical and/or experimental methods, which were originally conducted at different scales. By integrating these two methods through data assimilation, we are working on new applications of numerical simulations. The following figures show our research on obtaining interfacial and grain boundary properties by integrating molecular dynamics (MD) and phase-field (PF) methods through data assimilation.
Y. Nagatsuma, M. Ohno, T. Takaki, Y. Shibuta, Bayesian Data Assimilation of Temperature Dependence of Solid–Liquid Interfacial Properties of Nickel, Nanomaterials 11 (2021) 2308.
https://doi.org/10.3390/nano11092308
E. Miyoshi, M. Ohno, Y. Shibuta, A. Yamanaka, T. Takaki, Novel estimation method for anisotropic grain boundary properties based on Bayesian data assimilation and phase-field simulation, Materials & Design 210 (2021) 110089.
https://doi.org/10.1016/j.matdes.2021.110089
M. Ohno, Y. Oka, S. Sakane, Y. Shibuta, T. Takaki, Bayesian inference of solid-liquid interfacial properties out of equilibrium, Physical Review E 101 (2020) 052121.
https://doi.org/10.1103/PhysRevE.101.052121
E. Miyoshi, T. Takaki, Y. Shibuta, M. Ohno, Bridging molecular dynamics and phase-field methods for grain growth prediction, Computational Materials Science 152 (2018) 118-124.
https://doi.org/10.1016/j.commatsci.2018.05.046
Development of Multi-phase-field Model for Multiphase Flow
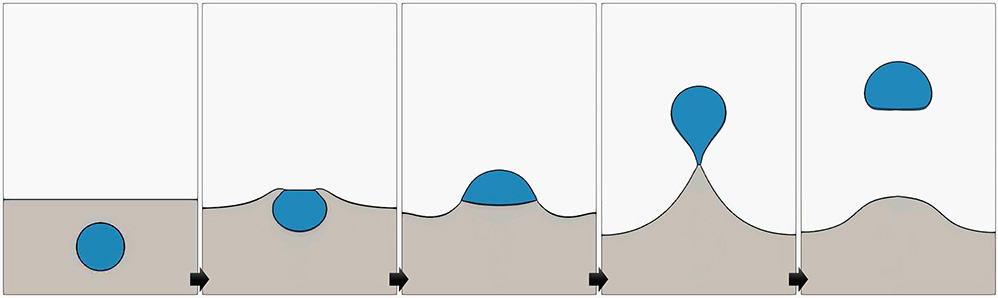
We develop a multi-phase-field model that enables the simulation of multi-phase flow with an arbitrary number of phases. The multi-phase-field model for multi-phase flow is expected to have various applications, such as drug discovery in drug delivery systems, evaluation of solid-gas-liquid three-phase flow in alloy solidification, and evaluation of multi-phase flow behavior with large deformation in vivo.
S. Aihara, T. Takaki, N. Takada, Multi-phase-field modeling using a conservative Allen–Cahn equation for multiphase flow, Computers & Fluids 178 (2019) 141-151.
https://doi.org/10.1016/j.compfluid.2018.08.023
Microstructure Prediction in Galvanizing

Galvanizing is applied to metal surfaces for corrosion protection and aesthetic appearance. In the hot-dip galvanizing process, dendrites with unusual shapes (several tens of microns in thickness and several millimeters in diameter) grow in the thin coating film and form beautiful patterns called spangles. The phase-field method is used to elucidate the formation mechanism of the spangles.
T. Takaki, K. Wada, K. Ishii, H. Yasuda, Two-dimensional phase-field study for spangle texture formation in hot-dip galvanizing, Computational Materials Science 187 (2021) 110077.
https://doi.org/10.1016/j.commatsci.2020.110077
Phase-field Topology Optimization
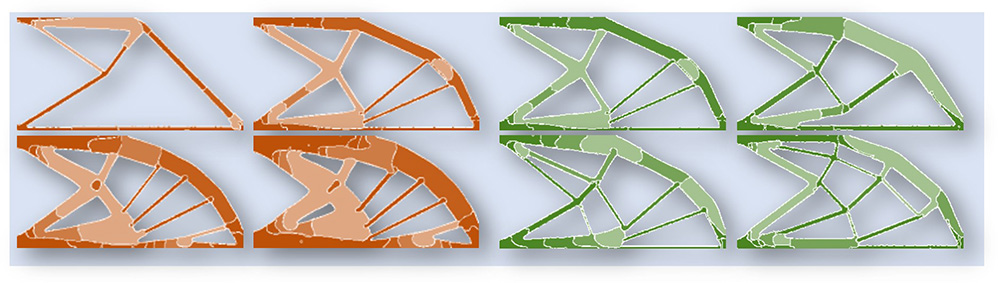
The most important aspects of structural design are strength and light weight. To increase strength, we can make the members thicker, but this makes the structure heavier. To improve the fuel efficiency of airplanes and automobiles, it is important to reduce the weight. In this case, it is necessary to aim for light materials as well as to design the shape and topology of the structure or to arrange multiple materials appropriately. We study the application of the phase-field method to a topology-optimization design for a structure with multiple materials.
T. Takaki, J. Kato, Phase-field topology optimization model that removes the curvature effects, Mechanical Engineering Journal 4 (2017) 16-00462-16-00462.
https://doi.org/10.1299/mej.16-00462
Phase-field Method and its Large-scale Simulation
Competitive Growth of Columnar Dendrites
Dendrite Growth with Liquid Flow
Growth of Equiaxed Dendrites with Motion
Permeability for Flow of Interdendritic Liquid
Development of AMR Phase-field Method
Multi-phase-field Simulation of Grain Growth
Data Assimilation Integrating MD and Phase-field Methods
Development of Multi-phase-field Model for Multiphase Flow







 /
/